Rotational spectroscopy
Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of
molecules in the
gas phase. The spectra of
polar molecules can be measured in
absorption or
emission by
microwave spectroscopy
[1] or by
far infrared
spectroscopy. The rotational spectra of non-polar molecules cannot be
observed by those methods, but can be observed and measured by
Raman spectroscopy. Rotational spectroscopy is sometimes referred to as
pure rotational spectroscopy to distinguish it from
rotational-vibrational spectroscopy
where changes in rotational energy occur together with changes in
vibrational energy, and also from ro-vibronic spectroscopy (or just
vibronic spectroscopy) where rotational, vibrational and electronic energy changes occur simultaneously.
For rotational spectroscopy, molecules are classified according to
symmetry into spherical top, linear and symmetric top; analytical
expressions can be derived for the rotational energy terms of these
molecules. Analytical expressions can be derived for the fourth
category, asymmetric top, for rotational levels up to J=3, but higher
energy levels need to be determined using numerical methods. The
rotational energies are derived theoretically by considering the
molecules to be
rigid rotors
and then applying extra terms to account for centrifugal distortion,
fine structure, hyperfine structure and Coriolis coupling. Fitting the
spectra to the theoretical expressions gives numerical values of the
angular
moments of inertia
from which very precise values of molecular bond lengths and angles can
be derived in favorable cases. In the presence of an electrostatic
field there is
Stark splitting which allows molecular
electric dipole moments to be determined.
An important application of rotational spectroscopy is in exploration of the chemical composition of the
interstellar medium using
radio telescopes.
Applications
Rotational spectroscopy has primarily been used to investigate
fundamental aspects of molecular physics. It is a uniquely precise tool
for the determination of molecular structure in gas phase molecules. It
can be used to establish barriers to internal rotation such as that
associated with the rotation of the
CH
3 group relative to the
C
6H
4Cl group in
chlorotoluene (
C
7H
7Cl).
[2]
When fine or hyperfine structure can be observed, the technique also
provides information on the electronic structures of molecules. Much of
current understanding of the nature of weak molecular interactions such
as
van der Waals,
hydrogen and
halogen bonds has been established through rotational spectroscopy. In connection with
radio astronomy, the technique has a key role in exploration of the chemical composition of the
interstellar medium. Microwave transitions are measured in the laboratory and matched to emissions from the
interstellar medium using a
radio telescope.
NH
3 was the first stable
polyatomic molecule to be identified in the
interstellar medium.
[3] The measurement of
chlorine monoxide[4] is important for
atmospheric chemistry.
Current projects in astrochemistry involve both laboratory microwave
spectroscopy and observations made using modern radiotelescopes such as
the
Atacama Large Millimetre Array (ALMA).
[5] Unlike
NMR,
Infrared and
UV-Visible spectroscopies, microwave spectroscopy has not yet found widespread application in
analytical chemistry.
Overview
A molecule in the
gas phase is free to rotate relative to a set of mutually
orthogonal axes of fixed orientation in space, centered on the
center of mass of the molecule. Free rotation is not possible for molecules in liquid or solid phases due to the presence of
intermolecular forces.
Rotation about each unique axis is associated with a set of quantized
energy levels dependent on the moment of inertia about that axis and a
quantum number. Thus, for linear molecules the energy levels are
described by a single moment of inertia and a single quantum number,

, which defines the magnitude of the rotational angular momentum.
For nonlinear molecules which are symmetric rotors (or symmetric tops
- see next section), there are two moments of inertia and the energy
also depends on a second rotational quantum number,

, which defines the vector component of rotational angular momentum along the
principal symmetry axis.
[6]
Analysis of spectroscopic data with the expressions detailed below
results in quantitative determination of the value(s) of the moment(s)
of inertia. From these precise values of the molecular structure and
dimensions may be obtained.
For a linear molecule, analysis of the rotational spectrum provides values for the
rotational constant[notes 2] and the moment of inertia of the molecule, and, knowing the atomic masses, can be used to determine the
bond length directly. For
diatomic molecules
this process is straightforward. For linear molecules with more than
two atoms it is necessary to measure the spectra of two or more
isotopologues, such as
16O
12C
32S and
16O
12C
34S. This allows a set of
simultaneous equations to be set up and solved for the
bond lengths).
[notes 3]
It should be noted that a bond length obtained in this way is slightly
different from the equilibrium bond length. This is because there is
zero-point energy
in the vibrational ground state, to which the rotational states refer,
whereas the equilibrium bond length is at the minimum in the potential
energy curve. The relation between the rotational constants is given by

where ν is a vibrational quantum number and α is a vibration-rotation
interaction constant which can be calculated if the B values for two
different vibrational states can be found.
[7]
For other molecules, if the spectra can be resolved and individual transitions assigned both
bond lengths and
bond angles
can be deduced. When this is not possible, as with most asymmetric
tops, all that can be done is to fit the spectra to three moments of
inertia calculated from an assumed molecular structure. By varying the
molecular structure the fit can be improved, giving a qualitative
estimate of the structure. Isotopic substitution is invaluable when
using this approach to the determination of molecular structure.
Classification of molecular rotors
In
quantum mechanics the free rotation of a molecule is
quantized, so that the
rotational energy and the
angular momentum can take only certain fixed values, which are related simply to the
moment of inertia,

, of the molecule. For any molecule, there are three moments of inertia:

,

and
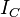
about three mutually orthogonal axes
A,
B, and
C with the origin at the
center of mass of the system. The general convention, used in this article, is to define the axes such that

, with axis

corresponding to the smallest moment of inertia. Some authors, however, define the

axis as the molecular
rotation axis of highest order.
The particular pattern of
energy levels
(and, hence, of transitions in the rotational spectrum) for a molecule
is determined by its symmetry. A convenient way to look at the molecules
is to divide them into four different classes, based on the symmetry of
their structure. These are
- Linear molecules. For a linear molecule the moments of inertia are related by
 . For most purposes,
. For most purposes,  can be taken to be zero. Examples of linear molecules include dioxygen, O
can be taken to be zero. Examples of linear molecules include dioxygen, O
2, dinitrogen, N
2, carbon monoxide, CO, hydroxy radical, OH, carbon dioxide, CO2, hydrogen cyanide, HCN, carbonyl sulfide, OCS, acetylene (ethyne, HC≡CH) and dihaloethynes. These molecules belong to the point groups C∞v or D∞h
- Symmetric tops (symmetric rotors) A symmetric top is a molecule in which two moments of inertia are the same,
 or
or  . By definition a symmetric top must have a 3-fold or higher order rotation axis. As a matter of convenience, spectroscopists divide molecules into two classes of symmetric tops, Oblate symmetric tops (saucer or disc shaped) with
. By definition a symmetric top must have a 3-fold or higher order rotation axis. As a matter of convenience, spectroscopists divide molecules into two classes of symmetric tops, Oblate symmetric tops (saucer or disc shaped) with  and Prolate symmetric tops (rugby football, or cigar shaped) with
and Prolate symmetric tops (rugby football, or cigar shaped) with  . The spectra look rather different, and are instantly recognizable. Examples of symmetric tops include
. The spectra look rather different, and are instantly recognizable. Examples of symmetric tops include
- Oblate: benzene, C
6H
6, ammonia, NH
3 - Prolate: chloromethane, CH
3Cl, propyne, CH
3C≡CH
- As a detailed example, ammonia has a moment of inertia IC = 4.4128 × 10−47 kg m2 about the 3-fold rotation axis, and moments IA = IB = 2.8059 × 10−47 kg m2 about any axis perpendicular to the C3 axis. Since the unique moment of inertia is larger than the other two, the molecule is an oblate symmetric top.[8]
- Asymmetric tops (asymmetric rotors) The three moments of inertia
have different values. Examples of small molecules that are asymmetric
tops include water, H
2O and nitrogen dioxide, NO
2 whose symmetry axis of highest order is a 2-fold rotation axis. Most large molecules are asymmetric tops.
Selection rules
Microwave and far-infrared spectra
Transitions between rotational states can be observed in molecules with a permanent
electric dipole moment.
[9][notes 4] A consequence of this rule is that no microwave spectrum can be observed for centrosymmetric linear molecules such as
N
2 (
dinitrogen) or HCCH (
ethyne), which are non-polar. Tetrahedral molecules such as
CH
4 (
methane),
which have both a zero dipole moment and isotropic polarizability,
would not have a pure rotation spectrum but for the effect of
centrifugal distortion; when the molecule rotates about a 3-fold
symmetry axis a small dipole moment is created, allowing a weak rotation
spectrum to be observed by microwave spectroscopy.
[10]
With symmetric tops, the selection rule for electric-dipole-allowed pure rotation transitions is Δ
K = 0, Δ
J = ±1. Since these transitions are due to absorption (or emission) of a single photon with a spin of one,
conservation of angular momentum implies that the molecular angular momentum can change by at most one unit.
[11] Moreover the quantum number
K is limited to have values between and including +
J to -
J.
[12]
Raman spectra
For
Raman spectra the molecules undergo transitions in which an
incident photon is absorbed and another
scattered photon is emitted. The general selection rule for such a transition to be allowed is that the molecular
polarizability must be
anisotropic, which means that it is not the same in all directions.
[13] Polarizability is a 3-dimensional
tensor
that can be represented as an ellipsoid. The polarizability ellipsoid
of spherical top molecules is in fact spherical so those molecules show
no rotational Raman spectrum. For all other molecules both
Stokes and anti-Stokes lines
[notes 5]
can be observed and they have similar intensities due to the fact that
many rotational states are thermally populated. The selection rule for
linear molecules is ΔJ = 0, ±2. The reason for the value of 2 is that
the polarizability returns to the same value twice during a rotation.
[14] The selection rule for symmetric top molecules is
- ΔK = 0
- If K = 0, then ΔJ = ±2
- If K ≠ 0, then ΔJ = 0, ±1, ±2
Transitions with Δ
J = +1 are said to belong the an
R series, whereas transitions with Δ
J = +2 belong to an
S series.
[15] Since Raman transitions involve two photons, it is possible for the molecular angular momentum to change by two units.
Units
The units used for rotational constants depend on the type of
measurement. With infrared spectra, the unit of measurement is usually
wavenumbers per cm, written as cm
−1 and shown with the symbol

.
Wavenumbers per cm is literally the number of waves in one centimeter,
or the reciprocal of wavelength in cm. On the other hand, microwave
spectra are usually measured in
Gigahertz. The relationship between the two units is derived from the expression

where ν is a
frequency, λ is a
wavelength and
c is the
velocity of light. It follows that

As 1 GHz = 10
9 Hz, the numerical conversion can be expressed as

Effect of vibration on rotation
The population of vibrationally excited states follows a Boltzmann
distribution, so low frequency vibrational states are appreciably
populated even at room temperatures. As the moment of inertia is higher
when a vibration is excited, the rotational constants,
B
decrease. Consequently, the rotation frequencies in each vibration state
are different from each other. This can give rise to "satellite" lines
in the rotational spectrum. An example is provided by
cyanodiacetylene, H-C≡C−C≡C-C≡N,
[16]
Further, there is a
fictitious force,
Coriolis coupling,
between the vibrational motion of the nuclei in the rotating
(non-inertial) frame. However, as long as the vibrational quantum number
does not change (i.e., the molecule is in only one state of vibration),
the effect of vibration on rotation is not important, because the time
for vibration is much shorter than the time required for rotation. The
Coriolis coupling is often negligible, too, if one is interested in low
vibrational and rotational quantum numbers only.
Effect of rotation on vibrational spectra
Historically, the theory of rotational energy levels was developed to
account for observations of vibration-rotation spectra of gases in
infrared spectroscopy,
which was used before microwave spectroscopy had become practical. To a
first approximation the energy of rotation is added to, or subtracted
from the energy of vibration. The vibration-rotation wavenumbers of
transitions for a harmonic oscillator with rigid rotor are given by
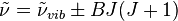
In reality, this expression has to be modified for the effects of
anharmonicity of the vibrations, for centrifugal distortion and for
Coriolis coupling.
[17] The plus sign implies simultaneous excitation of both vibration and rotation, giving the so-called
R
branch in the spectrum, whereas with the minus sign a quantum of
rotational energy is lost while a quantum of vibrational energy is
gained, giving the
P branch. The pure vibration, Δ
J=0, gives rise to the
Q branch of the spectrum. Because of the thermal population of the rotational states the
P branch is slightly less intense than the
R branch.
Rotational constants obtained from infrared measurements are in good
accord with those obtained by microwave spectroscopy while the latter
usually offers greater precision.
Structure of rotational spectra
Spherical top
Spherical top molecules have no net dipole moment. A pure rotational
spectrum cannot be observed by absorption or emission spectrocopy
because there is no permanent dipole moment whose rotation can be
accelerated by the electric field of an incident photon. Also the
polarizability is isotropic, so that pure rotational transitions cannot
be observed by Raman spectroscopy either. Nevertheless, rotational
constants can be obtained by
ro-vibrational spectroscopy. This occurs when a molecule is polar in the vibrationally excited state. For example, the molecule
methane
is a symmetric top but the asymmetric C-H stretching band shows
rotational fine structure in the infrared spectrum, illustrated in
rovibrational coupling. This spectrum is also interesting because it shows clear evidence of
Coriolis coupling in the asymmetric structure of the band.
Linear molecules
Energy levels and line positions calculated in the rigid rotor approximation
The
rigid rotor is a good starting point from which to construct a model of a rotating molecule. It is assumed that component atoms are
point masses
connected by rigid bonds. A linear molecule lies on a single axis and
each atom moves on the surface of a sphere around the centre of mass.
The two degrees of rotational freedom correspond to the
spherical coordinates
θ and φ which describe the direction of the molecular axis, and the
quantum state is determined by two quantum numbers J and M. J defines
the magnitude of the rotational angular momentum, and M its component
about an axis fixed in space, such as an external electric or magnetic
field. In the absence of external fields, the energy depends only on J.
Under the
rigid rotor model, the rotational energy levels,
F(J), of the molecule can be expressed as,

where

is the rotational constant of the molecule and is related to the moment
of inertia of the molecule. In a linear molecule the moment of inertia
about an axis perpendicular to the molecular axis is unique, that is,

, so
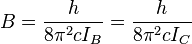
For a diatomic molecule
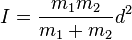
where
m1 and
m2 are the masses of the atoms and
d is the distance between them.
Selection rules dictate that during emission or absorption the rotational quantum number has to change by unity; i.e.,

. Thus, the locations of the lines in a rotational spectrum will be given by

where

denotes the lower level and

denotes the upper level involved in the transition.
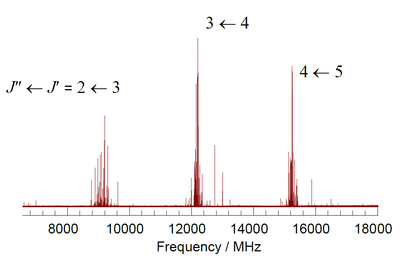
The diagram illustrates rotational transitions that obey the

=1 selection rule. The dashed lines show how these transitions map onto features that can be observed experimentally. Adjacent

transitions are separated by 2
B in the observed spectrum. Frequency or wavenumber units can also be used for the
x axis of this plot.
Rotational line intensities
Rotational level populations with Bhc/kT = 0.05. J is the quantum number of the lower rotational state
The probability of a transition taking place is the most important
factor influencing the intensity of an observed rotational line. This
probability is proportional to the population of the initial state
involved in the transition. The population of a rotational state depends
on two factors. The number of molecules in an excited state with
quantum number J, relative to the number of molecules in the ground
state,
NJ/N0 is given by the
Boltzmann distribution as
 ,
,
where k is the
Boltzmann constant and T the
absolute temperature. This factor decreases as J increases. The second factor is the
degeneracy of the rotational state, which is equal to 2J+1. This factor increases as J increases. Combining the two factors
[18]

The maximum relative intensity occurs at
[19][notes 6]

The diagram at the right shows an intensity pattern roughly corresponding to the spectrum above it.
Centrifugal distortion
When a molecule rotates, the
centrifugal force pulls the atoms apart. As a result, the moment of inertia of the molecule increases, thus decreasing the value of

,
when it is calculated using the expression for the rigid rotor. To
account for this a centrifugal distortion correction term is added to
the rotational energy levels of the diatomic molecule.
[20]

where

is the centrifugal distortion constant.
Therefore, the line positions for the rotational mode change to

In consequence, the spacing between lines is not constant, as in the
rigid rotor approximation, but decreases with increasing rotational
quantum number.
An assumption underlying these expressions is that the molecular vibration follows
simple harmonic motion. In the harmonic approximation the centrifugal constant

can be derived as

where
k is the vibrational
force constant. The relationship between

and

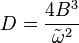
where :

is the harmonic vibration frequency, follows. If anharmonicity is to be
taken into account, terms in higher powers of J should be added to the
expressions for the energy levels and line positions.
[20] A striking example concerns the rotational spectrum of
hydrogen fluoride which was fitted to terms up to
[J(J+1)]5.
[21]
Oxygen
The electric dipole moment of the dioxygen molecule,
O
2 is zero, but the molecule is
paramagnetic
with two unpaired electrons so that there are magnetic-dipole allowed
transitions which can be observed by microwave spectroscopy. The unit
electron spin has three spatial orientations with respect to the given
molecular rotational angular momentum vector, K, so that each rotational
level is split into three states, J = K + 1, K, and K - 1, each J state
of this so-called p-type triplet arising from a different orientation
of the spin with respect to the rotational motion of the molecule. The
energy difference between successive J terms in any of these triplets is
about 2 cm
−1 (60 GHz), with the single exception of J = 1←0 difference which is about 4 cm
−1.
Selection rules for magnetic dipole transitions allow transitions
between successive members of the triplet (ΔJ = ±1) so that for each
value of the rotational angular momentum quantum number K there are two
allowed transitions. The
16O nucleus has zero nuclear spin angular momentum, so that symmetry considerations demand that K have only odd values.
[22][23]
Symmetric top
For symmetric rotors a quantum number
J is associated with the total angular momentum of the molecule. For a given value of J, there is a 2
J+1- fold degeneracy with the quantum number,
M taking the values +
J ...0 ... -
J. The third quantum number,
K is associated with rotation about the
principal rotation axis
of the molecule. In the absence of an external electrical field, the
rotational energy of a symmetric top is a function of only J and K and,
in the rigid rotor approximation, the energy of each rotational state is
given by

where

and

for a
prolate symmetric top molecule or

for an
oblate molecule.
This gives the transition wavenumbers as

which is the same as in the case of a linear molecule.
[24] With a first order correction for centrifugal distortion the transition wavenumbers become
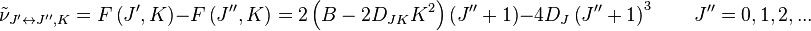
The term in
DJK has the effect of removing degeneracy present in the rigid rotor approximation, with different
K values.
[25]
Asymmetric top
Pure rotation spectrum of atmospheric water vapour measured at Mauna Kea (33 cm−1 to 100 cm−1)
The quantum number
J refers to the total angular momentum, as
before. Since there are three independent moments of inertia, there are
two other independent quantum numbers to consider, but the term values
for an asymmetric rotor cannot be derived in closed form. They are
obtained by individual
matrix diagonalization for each
J value. Formulae are available for molecules whose shape approximates to that of a symmetric top.
[26]
The water molecule is an important example of an asymmetric top. It
has an intense pure rotation spectrum in the far infrared region, below
about 200 cm
−1. For this reason far infrared spectrometers
have to be freed of atmospheric water vapour either by purging with a
dry gas or by evacuation. The spectrum has been analyzed in detail.
[27]
Quadrupole splitting
When a nucleus has a
spin quantum number,
I, greater than 1/2 it has a
quadrupole
moment. In that case, coupling of nuclear spin angular momentum with
rotational angular momentum causes splitting of the rotational energy
levels. If the
quantum number J of a rotational level is greater than
I, 2
I+1 levels are produced; but if
J is less than
I, 2
J+1 levels result. The effect is known as
hyperfine splitting. For example, with
14N (
I = 1) in HCN, all levels with J > 0 are split into 3. The energy of the sub-levels are proportional to the
nuclear quadrupole moment and a function of
F and
J. where
F =
J+
I,
J+
I-1, ..., 0, ... |
J-
I|. Thus, observation of nuclear quadrupole splitting permits the magnitude of the nuclear quadrupole moment to be determined.
[28] This is an alternative method to the use of
nuclear quadrupole resonance spectroscopy. The selection rule for rotational transitions becomes
[29]

Stark and Zeeman effects
In the presence of a static external
electric field the 2
J+1 degeneracy of each rotational state is partly removed, an instance of a
Stark effect. For example in linear molecules each energy level is split into
J+1
components. The extent of splitting depends on the square of the
electric field strength and the square of the dipole moment of the
molecule.
[30] In principle this provides a means to determine the value of the molecular dipole moment with high precision. Examples include
carbonyl sulfide, OCS, with μ = 0.71521 ± 0.00020
Debye. However, because the splitting depends on μ
2, the orientation of the dipole must be deduced from quantum mechanical considerations.
[31]
A similar removal of degeneracy will occur when a
paramagnetic molecule is placed in a magnetic field, an instance of the
Zeeman effect. Most species which can be observed in the gaseous state are
diamagnetic . Exceptions, known as
odd molecules, include
nitric oxide, NO,
nitrogen dioxide,
NO
2, some
chlorine oxides and the
hydroxyl radical. The Zeeman effect has been observed with
dioxygen,
O
2[32]
Rotational Raman spectroscopy
Molecular rotational transitions can also be observed by
Raman spectroscopy. Rotational transitions are Raman-allowed for any molecule with an
anisotropic polarizability
which includes all molecules except for spherical tops. This means that
rotational transitions of molecules with no permanent dipole moment,
which cannot be observed in absorption or emission, can be observed, by
scattering, in Raman spectroscopy. Very high resolution Raman spectra
can be obtained by adapting a
Fourier Transform Infrared Spectrometer. An example is the spectrum of
15N
2. It shows the effect of nuclear spin, resulting in
intensities variation of 3:1 in adjacent lines. A bond length of
109.9985 ± 0.0010 pm was deduced from the data.
[33]
Instruments and Methods
The great majority of contemporary spectrometers use a mixture of
commercially available and bespoke components which users integrate
according to their particular needs. Instruments can be broadly
categorised according to their general operating principals. Although
rotational transitions can be found across a very broad region of the
electromagnetic spectrum,
fundamental physical constraints exist on the operational bandwidth of
instrument components. It is often impractical and costly to switch to
measurements within an entirely different frequency region. The
instruments and operating principals described below are generally
appropriate to microwave spectroscopy experiments conducted at
frequencies between 6 and 24 GHz.
Absorption cells and Stark modulation
A microwave spectrometer can be most simply constructed using a
source of microwave radiation, an absorption cell into which sample gas
can be introduced and a detector such as a
superheterodyne receiver.
A spectrum can be obtained by sweeping the frequency of the source
while detecting the intensity of transmitted radiation. A simple section
of
waveguide
can serve as an absorption cell. An important variation of the
technique in which an alternating current is applied across electrodes
within the absorption cell results in a modulation of the frequencies of
rotational transitions. This is referred to as Stark modulation and
allows the use of
phase-sensitive detection
methods offering improved sensitivity. Absorption spectroscopy allows
the study of samples that are thermodynamically stable at room
temperature. The first study of the
microwave spectrum of a molecule (
NH
3) was performed by Cleeton & Williams in 1934.
[34] Subsequent experiments exploited powerful sources of
microwaves such as the
klystron, many of which were developed for
radar during the
Second World War. The number of experiments in microwave spectroscopy surged immediately after the war. By 1948,
Walter Gordy was able to prepare a review of the results contained in approximately 100 research papers.
[35] Commercial versions
[36] of microwave absorption spectrometer were developed by
Hewlett Packard in the 1970s and were once widely used for fundamental research. Most research laboratories now exploit either Balle-
Flygare or chirped-pulse Fourier transform microwave (FTMW) spectrometers.
Fourier transform microwave (FTMW) spectroscopy
The theoretical framework
[37] underpinning FTMW spectroscopy is analogous to that used to describe
FT-NMR spectroscopy. The behaviour of the evolving system is described by optical
Bloch equations.
First, a short (typically 0-3 microsecond duration) microwave pulse is
introduced on resonance with a rotational transition. Those molecules
that absorb the energy from this pulse are induced to rotate coherently
in phase with the incident radiation. De-activation of the polarisation
pulse is followed by microwave emission that accompanies decoherence of
the molecular ensemble. This
free induction decay
occurs on a timescale of 1-100 microseconds depending on instrument
settings. Following pioneering work by Dicke and co-workers in the
1950s,
[38] the first FTMW spectrometer was constructed by Ekkers and
Flygare in 1975.
[39]
The Balle-Flygare FTMW spectrometer
Balle, Campbell, Keenan and Flygare demonstrated that the FTMW
technique can be applied within a "free space cell" comprising an
evacuated chamber containing a
Fabry-Perot cavity.
[40] This technique allows a sample to be probed only milliseconds after it undergoes rapid cooling to only a few
kelvins
in the throat of an expanding gas jet. This was a revolutionary
development because (i) cooling molecules to low temperatures
concentrates the available population in the lowest rotational energy
levels. Coupled with benefits conferred by the use of a Fabry-Perot
cavity, this brought a great enhancement in the sensitivity and
resolution of spectrometers along with a reduction in the complexity of
observed spectra; (ii) it became possible to isolate and study molecules
that are very weakly bound because there is insufficient energy
available for them to undergo fragmentation or chemical reaction at such
low temperatures.
William Klemperer
was a pioneer in using this instrument for the exploration of weakly
bound interactions. While the Fabry-Perot cavity of a Balle-Flygare FTMW
spectrometer can typically be tuned into resonance at any frequency
between 6 and 18 GHz, the bandwidth of individual measurements is
restricted to about 1 MHz. An animation illustrates the operation of
this instrument which is currently the most widely used tool for
microwave spectroscopy.
[41]
The Chirped-Pulse FTMW spectrometer
Noting that digitisers and related electronics technology had
significantly progressed since the inception of FTMW spectroscopy,
B.H. Pate at the University of Virginia
[42] designed a spectrometer
[43]
which retains many advantages of the Balle-Flygare FT-MW spectrometer
while innovating in (i) the use of a high speed (>4 GS/s) arbitrary
waveform generator to generate a "chirped" microwave polarisation pulse
that sweeps up to 12 GHz in frequency in less than a microsecond and
(ii) the use of a high speed (>40 GS/s) oscilloscope to digitise and
Fourier transform the molecular free induction decay. The result is an
instrument that allows the study of weakly bound molecules but which is
able to exploit a measurement bandwidth (12 GHz) that is greatly
enhanced compared with the Balle-Flygare FTMW spectrometer. Modified
versions of the original CP-FTMW spectrometer have been constructed by a
number of groups in the United States, Canada and Europe.
[44][45]
The instrument offers a broadband capability that is highly
complementary to the high sensitivity and resolution offered by the
Balle-Flygare design.
Notes
The
spectrum was measured over a couple of hours with the aid of a
chirped-pulse Fourier transform microwave spectrometer at the University
of Bristol.
This article uses the molecular spectroscopist's convention of expressing the rotational constant  in cm-1. Therefore
in cm-1. Therefore  in this article corresponds to
in this article corresponds to  in the Rigid rotor article.
in the Rigid rotor article.
For
a symmetric top, the values of the 2 moments of inertia can be used to
derive 2 molecular parameters. Values from each additional isotopologue
provide the information for one more molecular parameter. For asymmetric
tops a single isotopologue provides information for at most 3 molecular
parameters.
Such
transitions are called electric dipole-allowed transitions. Other
transitions involving quadrupoles, octupoles, hexadecapoles etc. may
also be allowed but the spectral intensity is very much smaller, so
these transitions are difficult to observe. Magnetic-dipole-allowed
transitions can occur in paramagnetic molecules such as dioxygen, O
2 and nitric oxide, NO
In
Raman spectroscopy the photon energies for Stokes and anti-Stokes
scattering are respectively less than and greater than the incident
photon energy. See the energy-level diagram at Raman spectroscopy.
- This
value of J corresponds to the maximum of the population considered as a
continuous function of J. However, since only integer values of J are
allowed, the maximum line intensity is observed for a neighboring
integer J.
References
Gordy, W. (1970). A. Weissberger, ed. Microwave Molecular Spectra in Technique of Organic Chemistry IX. New York: Interscience.
Nair,
K.P.R.; Demaison, J.; Wlodarczak, G.; Merke, I. (236). "Millimeterwave
rotational spectrum and internal rotation in o-chlorotoluene". Journal of Molecular Spectroscopy 237 (2): 137–142. Bibcode:2006JMoSp.237..137N. doi:10.1016/j.jms.2006.03.011.
Cheung, A.C.; Rank, D.M.; Townes, C.H.; Thornton, D.D. & Welch, W.J. (1968). "Detection of NH
3 molecules in the interstellar medium by their microwave emission spectra". Physical Review Letters 21 (25): 1701–5. Bibcode:1968PhRvL..21.1701C. doi:10.1103/PhysRevLett.21.1701.
Ricaud,
P.; Baron, P; de La Noë, J. (2004). "Quality assessment of ground-based
microwave measurements of chlorine monoxide, ozone, and nitrogen
dioxide from the NDSC radiometer at the Plateau de Bure". Ann. Geophys 22: 1903–15. Bibcode:2004AnGeo..22.1903R. doi:10.5194/angeo-22-1903-2004.
"Astrochemistry in Virginia". Retrieved 2 December 2012.
Atkins & de Paula 2006, p. 444
Banwell & McCash 1994, p. 99
Moment of inertia values from Atkins & de Paula 2006, p. 445
Hollas 1996, p. 95
Hollas 1996, p. 104 shows part of the observed rotational spectrum of silane
Atkins & de Paula 2006, p. 447
Banwell & McCash 1994, p. 49
Hollas 1996, p. 111
Atkins & de Paula 2006, p. 474–5
Banwell & McCash 1994, Section 4.2, p. 105, Pure Rotational Raman Spectra
Alexander,
A.J; Kroto, H.W; Walton, D.R.M. (1967). "The microwave spectrum,
substitution structure and dipole moment of cyanobutadiyne". J. Mol. Spectrosc 62: 175–180. Bibcode:1976JMoSp..62..175A. doi:10.1016/0022-2852(76)90347-7. Illustrated in Hollas 1996, p. 97
Banwell & McCash 1994, p. 63
Banwell & McCash 1994, p. 40
Atkins & de Paula 2006, p. 449
Banwell & McCash 1994, p. 45
Jennings,
D.A.; Evenson, K.M; Zink, L.R.; Demuynck, C.; Destombes, J.L.; Lemoine,
B; Johns,J.W.C. (April 1987). "High-resolution spectroscopy of HF from
40 to 1100 cm−1: Highly accurate rotational constants". Journal of Molecular Spectroscopy 122 (2): 477–480. Bibcode:1987JMoSp.122..477J. doi:10.1016/0022-2852(87)90021-X.pdf
Strandberg, M. W. P.; Meng, C. Y.; Ingersoll, J. G. (1949). "The Microwave Absorption Spectrum of Oxygen". Phys.Rev. 75 (10): 1524–8. Bibcode:1949PhRv...75.1524S. doi:10.1103/PhysRev.75.1524.pdf
Krupenie, Paul H. (1972). "The Spectrum of Molecular Oxygen" (PDF). J. Phys. Chem. Ref. Data 1, 423 (1972) 1 (2): 423–534. Bibcode:1972JPCRD...1..423K. doi:10.1063/1.3253101.
Hollas 1996, p. 101
Hollas 1996, p. 102 shows the effect on the microwave spectrum of H
3SiNCS.
Hollas 1996, p. 103
Hall, Richard T.; Dowling, Jerome M. (1967). "Pure Rotational Spectrum of Water Vapor". J. Chem. Phys. 47 (7): 2454–61. Bibcode:1967JChPh..47.2454H. doi:10.1063/1.1703330. Hall, Richard T.; Dowling, Jerome M. (1971). "Erratum: Pure Rotational Spectrum of Water Vapor". J. Chem. Phys. 54 (11): 4968. Bibcode:1971JChPh..54.4968H. doi:10.1063/1.1674785.
Simmons, James W.; Anderson, Wallace E.; Gordy,Walter (1950). "Microwave Spectrum and Molecular Constants of Hydrogen Cyanide". Phys. Rev. 77: 77–79. Bibcode:1950PhRv...77...77S. doi:10.1103/PhysRev.77.77.
Chang, Raymond (1971). Basic Principles of Spectroscopy. McGraw-Hill. p139
Hollas 1996, p. 102 gives the equations for diatomic molecules and symmetric tops
Hollas 1996, p. 102
Burkhalter,
James H.; Roy S. Anderson; William V. Smith; Walter Gordy (1950). "The
Fine Structure of the Microwave Absorption Spectrum of Oxygen". Phys. Rev. 79 (4): 651–5. Bibcode:1950PhRv...79..651B. doi:10.1103/PhysRev.79.651.
Hollas 1996, p. 113, illustrates the spectrum of 15N
2 obtained using 476.5 nm radiation from an argon ion laser.
Cleeton, C.E.; Williams, N.H. (1934). "Electromagnetic waves of 1.1 cm wave-length and the absorption spectrum of ammonia". Physical Reviews 45 (4): 234–7. Bibcode:1934PhRv...45..234C. doi:10.1103/PhysRev.45.234.
Gordy, W. (1948). "Microwave spectroscopy". Reviews of Modern Physics 20 (4): 668–717. Bibcode:1948RvMP...20..668G. doi:10.1103/RevModPhys.20.668.
"June 1971, Hewlett Packard Journal" (PDF). Retrieved November 2012.
Schwendemann, R.H. (1978). "Transient Effects in Microwave Spectroscopy". Ann. Rev. Phys. Chem. 29: 537–558. Bibcode:1978ARPC...29..537S. doi:10.1146/annurev.pc.29.100178.002541.
Dicke, R.H.; Romer, R.H. (1955). "Pulse Techniques in Microwave Spectroscopy". Rev. Sci. Inst. 26 (10): 915–928. Bibcode:1955RScI...26..915D. doi:10.1063/1.1715156.
Ekkers, J.; Flygare, W.H. (1976). "Pulsed microwave Fourier transform spectrometer". Rev. Sci. Inst. 47 (4): 448–454. Bibcode:1976RScI...47..448E. doi:10.1063/1.1134647.
Balle,
T.J.; Campbell, E.J.; Keenan, M.R.; Flygare, W.H. (1980). "A new method
for observing the rotational spectra of weak molecular complexes:
KrHCl". J. Chem. Phys. 72 (2): 922–932. Bibcode:1980JChPh..72..922B. doi:10.1063/1.439210.
Jager, W. "Balle-Flygare FTMW spectrometer animation".
"Web page of B.H. Pate Research Group, Department of Chemistry, University of Virginia". Retrieved November 2012.
Brown,
G.G.; Dian, B.C.; Douglass, K.O.; Geyer, S.M.; Pate, B.H. (2006). "The
rotational spectrum of epifluorohydrin measured by chirped-pulse Fourier
transform microwave spectroscopy". J. Mol. Spectrosc. 238: 200–212. Bibcode:2006JMoSp.238..200B. doi:10.1016/j.jms.2006.05.003.
Grubbs,
G.S.; Dewberry, C.T.; Etchison, K.C.; Kerr, K.E.; Cooke, S.A. (2007).
"A search accelerated correct intensity Fourier transform microwave
spectrometer with pulsed laser ablation source". Rev. Sci. Inst. 78 (9): 096106. Bibcode:2007RScI...78i6106G. doi:10.1063/1.2786022.
- Wilcox, D.S.; Hotopp, K.M.; Dian, B.C. (2011). "Two-Dimensional Chirped-Pulse Fourier Transform Microwave Spectroscopy". J. Phys. Chem. A 115 (32): 8895–8905. doi:10.1021/jp2043202.
Bibliography
- Atkins, P. W.; de Paula, J. (2006). "Molecular Spectroscopy: Section: Pure rotation spectra". Physical Chemistry (8th ed.). Oxford University Press. pp. 431–469. ISBN 0198700725.
- Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentals of Molecular Spectroscopy (4th ed.). McGraw-Hill. ISBN 0-07-707976-0.
- Brown, John M.; Carrington, Alan (2003). Rotational spectroscopy of diatomic molecule. Cambridge University Press. ISBN 0-521-53078-4.
- Hollas, M. J. (1996). Modern Spectroscopy (3rd ed.). Wiley. ISBN 0471965227.
- Kroto, H. W. (2003). Molecular Rotation Spectroscopy. Dover. ISBN 0-486-49540-X.
- McQuarrie, Donald A. (2008). Quantum Chemistry. University Science Books. ISBN 1-891389-50-5.
- Townes, Charles H.; Schawlow, Arthur L. (1975). Microwave Spectroscopy. Dover. ISBN 978-0-486-61798-5.
- Kovács, István (1969). Rotational Structure in the Spectra of Diatomic Molecules. Adam Hilger. ISBN 0852741421.
- Wollrab, James E. (1967). Rotational spectra and molecular structure. Academic Press. ISBN 148319485X.
External links
TAKE A TOUR
Con Dao Island, Vietnam

Con Dao Island, Vietnam
This 16-island archipelago is a “pocket of paradise,” says Robert Reid, a travel editor at
Lonely Planet.
Getting there: Take a 45-minute flight from Ho Chi Minh City.
What to do: The
diving is among the best in Vietnam. Take scuba lessons as a couple or
discover the nearby secluded beaches of Bai Dat Doc and Dam Trau.
Where to stay: Six Senses
resort offers luxury villas on the East Vietnam Sea. The resort has an
in-house spa offering traditional Vietnamese healing practices; it also
boasts outdoor treatment rooms and a yoga and meditation pavilion.
Inquire for rates.
wikitravel.org/en/Con_Dao
Con Dao is an
island off the southern coast of
Vietnam. ... The
Con Dao Islands separated from the mainland about 15,000 years ago. This has resulted in the ...

.

airport
////////////



 airport
airport




 , which defines the magnitude of the rotational angular momentum.
, which defines the magnitude of the rotational angular momentum. , which defines the vector component of rotational angular momentum along the
, which defines the vector component of rotational angular momentum along the 
 , of the molecule. For any molecule, there are three moments of inertia:
, of the molecule. For any molecule, there are three moments of inertia:  ,
,  and
and 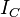 about three mutually orthogonal axes A, B, and C with the origin at the
about three mutually orthogonal axes A, B, and C with the origin at the  , with axis
, with axis  corresponding to the smallest moment of inertia. Some authors, however, define the
corresponding to the smallest moment of inertia. Some authors, however, define the  . Examples of spherical tops include
. Examples of spherical tops include  . For most purposes,
. For most purposes,  or
or  . By definition a symmetric top must have a 3-fold or higher order
. By definition a symmetric top must have a 3-fold or higher order  and
and  . The spectra look rather different, and are instantly recognizable. Examples of symmetric tops include
. The spectra look rather different, and are instantly recognizable. Examples of symmetric tops include .
Wavenumbers per cm is literally the number of waves in one centimeter,
or the reciprocal of wavelength in cm. On the other hand, microwave
spectra are usually measured in
.
Wavenumbers per cm is literally the number of waves in one centimeter,
or the reciprocal of wavelength in cm. On the other hand, microwave
spectra are usually measured in 


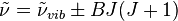


 is the rotational constant of the molecule and is related to the moment
of inertia of the molecule. In a linear molecule the moment of inertia
about an axis perpendicular to the molecular axis is unique, that is,
is the rotational constant of the molecule and is related to the moment
of inertia of the molecule. In a linear molecule the moment of inertia
about an axis perpendicular to the molecular axis is unique, that is,  , so
, so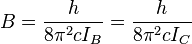
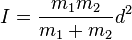
 . Thus, the locations of the lines in a rotational spectrum will be given by
. Thus, the locations of the lines in a rotational spectrum will be given by
 denotes the lower level and
denotes the lower level and  denotes the upper level involved in the transition.
denotes the upper level involved in the transition. =1 selection rule. The dashed lines show how these transitions map onto features that can be observed experimentally. Adjacent
=1 selection rule. The dashed lines show how these transitions map onto features that can be observed experimentally. Adjacent  transitions are separated by 2B in the observed spectrum. Frequency or wavenumber units can also be used for the x axis of this plot.
transitions are separated by 2B in the observed spectrum. Frequency or wavenumber units can also be used for the x axis of this plot.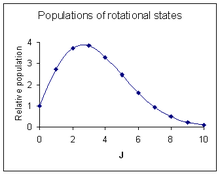
 ,
,


 is the centrifugal distortion constant.
is the centrifugal distortion constant.

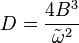
 is the harmonic vibration frequency, follows. If anharmonicity is to be
taken into account, terms in higher powers of J should be added to the
expressions for the energy levels and line positions.
is the harmonic vibration frequency, follows. If anharmonicity is to be
taken into account, terms in higher powers of J should be added to the
expressions for the energy levels and line positions.
 and
and  for a prolate symmetric top molecule or
for a prolate symmetric top molecule or  for an oblate molecule.
for an oblate molecule.
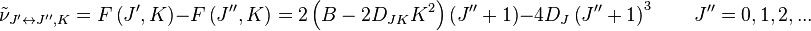


 in the Rigid rotor article.
in the Rigid rotor article.